The Cronbach’s Alphas for all the scales in my path analysis are in the .7s, so why is a reviewer criticizing me for not paying sufficient attention to reliability?
 The issue of reliability can be a complex and often misunderstood issue. Entire text books have been written about reliability, validity, and scale construction, so we only briefly touch on the key issues here (see Bandalos, 2018, for an excellent recent example). To begin, in most areas across the behavioral, educational, and health sciences, theoretical constructs are hypothesized to exist yet cannot be directly measured. Common examples include depression, anxiety, academic motivation, commitment to treatment, and perceived stress. A vast array of psychometric methods have been developed over the past century to use multi-item scales as a basis to infer the existence of these underlying constructs. Indeed, the genesis of factor analysis (most commonly dated to Spearman in 1903) was motivated by the desire to use multi-test assessments to compute person-specific values of cognitive functioning. Psychometric methods are sometimes organized into pragmatic approaches (e.g., Classical Test Theory) and axiomatic approaches (e.g., item response theory and factor analysis). However, a fundamental component of all of these methods is reliability.
The issue of reliability can be a complex and often misunderstood issue. Entire text books have been written about reliability, validity, and scale construction, so we only briefly touch on the key issues here (see Bandalos, 2018, for an excellent recent example). To begin, in most areas across the behavioral, educational, and health sciences, theoretical constructs are hypothesized to exist yet cannot be directly measured. Common examples include depression, anxiety, academic motivation, commitment to treatment, and perceived stress. A vast array of psychometric methods have been developed over the past century to use multi-item scales as a basis to infer the existence of these underlying constructs. Indeed, the genesis of factor analysis (most commonly dated to Spearman in 1903) was motivated by the desire to use multi-test assessments to compute person-specific values of cognitive functioning. Psychometric methods are sometimes organized into pragmatic approaches (e.g., Classical Test Theory) and axiomatic approaches (e.g., item response theory and factor analysis). However, a fundamental component of all of these methods is reliability.
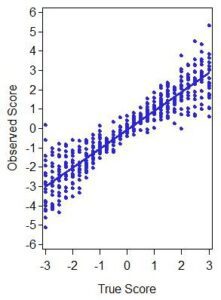
Reliability addresses the issue of consistency of measurement and is centered on the belief that an observed score is some combination of unobserved true score and error (e.g., DeVellis, 2016). Reliability can then be defined in terms of the relative magnitude of these two components. Many conceptual definitions of reliability have been proposed, but the most widely used is the ratio of true score variance to total observed variance. Thus a reliability of 1.0 reflects that all of the observed variability is true score variability and there is no error of measurement. However, as reliability falls below 1.0 this indicates that more and more of the observed variability is due to measurement error. The posed question notes reliability values in the .7’s, and this indicates that as much as 30% of the observed variability in the measured variables is due to error. This is a non-trivial amount of error that can have potentially profound implications in subsequent model fitting.
For example, all members of the general linear model (ANOVA, multiple regression, path analysis, etc.) assume that predictors are measured with perfect reliability (the precise assumption is that the distributions of predictors are “fixed and known” but this in turn implies perfect reliability). Violation of this assumption leads to biased regression coefficients. With just one predictor, the biasing effect of measurement error is always to attenuate coefficient estimates; that is, sample estimates become systematically smaller than the actual population values as the degree of unreliability of the predictor increases (Bollen, 1989, pp. 167-168). With two or more predictors, the direction and magnitude of bias is harder to predict (Bollen & Schwing, 1987). Further, although unreliability in an outcome measure does not bias the raw regression coefficients, it does distort standardized effect estimates and leads to inflated standard errors that reduce power. Taken together, violation of the assumption of perfect reliability when using manifest scale scores can result in substantially biased parameter estimates and markedly lower statistical power, concerns that are implied by the reviewer’s critique.
Two challenges thus arise: how to best empirically compute reliability and how to best account for unreliability in analyses. McNeish (2018) offers a recent comprehensive review of the first question. Historically, coefficient alpha (or “Cronbach’s Alpha”) has become the standard empirical measure of reliability in the social and health sciences. However, alpha is based on several strict and untenable assumptions that often drive down the estimated value such that coefficient alpha is often viewed as a “lower bound” reliability estimate. Other methods of estimation exist (e.g., Omega, coefficient H, Greatest Lower Bound) but each of these is associated with certain limitations. Further, all of these are associated with a classical test theory approach in which there is a single reliability estimate across the range of scale scores. In contrast, axiomatic approaches such as IRT expand this conceptualization such that reliability depends in part on the underlying score itself (e.g., Thissen & Wainer, 2001, pp. 1178-119). For example, reliability decreases with extreme scores at the lowest and highest parts of the latent trait distribution, and these differences are not reflected within the CTT framework.
Regardless of how it is computed, the second issue remains: how to account for imperfect reliability in subsequent analysis. The ideal option is to move from a manifest variable model to a latent variable model (e.g., Bollen, 2002). Here, multiple-indicator latent factors are defined in place of a mean or sum score. This allows for the estimation of measurement error and the separation of true score variability from error variability. Latent variables add complexity to any model and thus an informed decision is needed as to the relative gains achieved relative to the loss of parsimony. When it is not possible to simultaneously estimate a full latent variable model, an alternative is to try to adjust for unreliability in scale scores when conducting the path analysis. Various options for correcting for unreliability have been proposed in the literature, and this remains an active area of research (e.g., Devlieger, 2019).
Returning to the question about the reviewer’s criticism, it is true that simply reporting coefficient alpha values with an unsupported subjective judgment that the obtained values are “adequate” does not address the complexity of the issues at hand. First, it is helpful to consider whether coefficient alpha is the optimal method of reliability estimation or if there are other better options available. Second, if reliability estimates are less than 1.0, it should be communicated to the reader exactly what implications this has on subsequent modeling and inferential tests. Finally, if scales are determined to have meaningful levels of unreliability (whatever that is judged to be), then expanding the modeling framework to include multiple-indicator latent factors should be closely considered.
References
Bandalos, D. L. (2018). Measurement theory and applications for the social sciences. Guilford Publications.
Bollen, K. A. (1989). Structural Equations with Latent Variables. John Wiley New York.
Bollen, K. A. (2002). Latent variables in psychology and the social sciences. Annual Review of Psychology, 53, 605-634.
Bollen, K. A., & Schwing, R. C. (1987). Air pollution-mortality models: A demonstration of the effects of random measurement error. Quality and Quantity, 21, 37-48.
DeVellis, R. F. (2016). Scale development: Theory and applications (Vol. 26). Sage publications.
Devlieger, I., Talloen, W., & Rosseel, Y. (2019). New Developments in Factor Score Regression: Fit Indices and a Model Comparison Test. Educational and Psychological Measurement, 79, 1017–1037.
McNeish, D. (2018). Thanks coefficient alpha, we’ll take it from here. Psychological Methods, 23, 412-433.
Thissen, D. & Wainer, H. (Eds.). (2001). Test scoring. L. Erlbaum Associates, Publishers.

