A reviewer recently asked me to comment on the issue of equivalent models in my structural equation model. What is the difference between alternative models and equivalent models within an SEM?
Differentiating between alternative models and equivalent models has long been a point of confusion in many research applications. Although the challenge of equivalent models can arise within almost any analytic setting, this is particularly salient within the structural equation model (or SEM). It is helpful first distinguish between alternative and equivalent models.
To begin, one of the greatest strengths of the SEM is the ability to estimate models in very specific ways to closely correspond to theory. Sometimes we can think of this as the “whiteboard” problem: we draw out our measured variables on the board and then connect them with single- and double-headed arrows and circles in a way that best reflects our theoretically-derived research hypotheses. We often build one model that is most consistent with our theory, but there are alternative models we might consider. Alternative models represent different path diagrams that make different statements about the underlying theory. A key strength of the SEM is that we can make formal comparisons of the fit of alternative models based on sample data: one model might attain superior fit when compared to another, providing empirical support for favoring the better fitting model versus the alternative.
In contrast, whereas alternative models almost always lead to differences in model fit, equivalent models are different representations of model structure that result in precisely the same model fit. That is, the models are equivalent representations of the sample data and cannot be distinguished from one another based on empirical fit. An equivalent model can be thought of as a re-parameterization of the original model. In other words, it is just a different way of “packaging” the same information in the data and no equivalent model can be distinguished from another based on fit alone. If you were to fit a series of equivalent models to the same sample data you obtain exactly the same chi-square test statistic, RMSEA, CFI, TLI, and any other omnibus measure of fit. (Side note: One thing that may be confusing is that, depending on how the models are estimated, their log-likelihoods might differ, but these differences will cancel out when computing measures of fit relative to the corresponding saturated or baseline models, thus their fit remains the same).
Take a very simple example: a three variable mediation model might state that the predictor leads to the mediator that in turn leads to the outcome; diagrammatically, this is portrayed as:
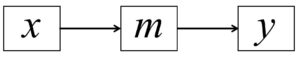
This model has one degree-of-freedom and will have obtain some degree of fit to the data (chi-square, RMSEA, CFI, etc.). However, there are two equivalent models that obtain precisely the same model fit when estimated using sample data. The first is:
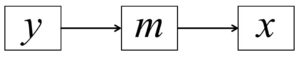
and the second is:
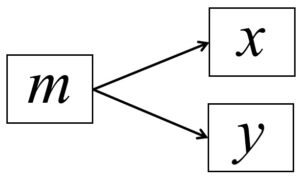
All three of these models make fundamentally different statements about the underlying model that gave rise to the observed data, yet all three fit precisely the same. As such, the three models are numerically equivalent and can only be adjudicated based on theory.
The above example only considers three measured variables with two regression coefficients. Imagine how this problem scales up with many more measures and many more parameters, particularly if a model includes one or more latent factors. Fortunately, much research has been conducted to help identify a set of existing equivalent models that accompany any given hypothesized model. Although several important papers have been written on this topic (e.g., Stelzl, 1986; MacCallum et al., 1993), a key contribution was made by Lee and Hershberger (1990) where they developed what are sometimes called “replacement rules” or just “Lee-Hershberger rules”. Briefly, Lee and Hershberger describe a very clever approach where variables in a given model can be organized into three blocks: a preceding block, a focal block, and a succeeding block. Then, within the focal block, a large number of modifications can be made to how the variables relate to one another (e.g., reversing pathways, changing regression coefficients to covariances), all of which will achieve identical model fit. A model of even modest complexity might have 50 corresponding alternative expressions, and more complex models can result in hundreds if not thousands of equivalent counterparts.
There are several core takeaway points here. First, it is important to realize that this is simply a characteristic of the SEM and is part of the price we pay for having the flexibility to parameterize models in precisely the way we desire. Second, very little can be done to empirically distinguish among equivalent models (given traditional measures of fit will be identical). Some specific suggestions have been offered (e.g., Raykov & Penev, 1999) but none are able to fully resolve the issue. Indeed, even replication with an independent sample does not resolve the issue because two equivalent models will attain identical fit within any given sample data.
As such, it is important that a researcher be unambiguously aware that this issue exists and to realize that any given hypothesized model is just one of an entire family of models, all of which are numerically indistinguishable in terms of model fit. Of course some of these models may not be theoretically plausible (e.g., a mediator predicting biological sex or a prediction back in time) but many dozens of options may remain. It is often best to treat this as a limitation of any given study and to potentially present one or a small number of equivalent model options to the reader so that these too might be considered as plausible representations of the data. Further, it might be beneficial to consider these issues when engineering future studies in which certain design elements might be incorporated to help reduce the universe of possible equivalent models.
References
Lee, S., & Hershberger, S. (1990). A simple rule for generating equivalent models in covariance structure modeling. Multivariate Behavioral Research, 25, 313-334.
MacCallum, R. C., Wegener, D. T., Uchino, B. N., & Fabrigar, L. R. (1993). The problem of equivalent models in applications of covariance structure analysis. Psychological Bulletin, 114, 185-199.
Raykov, T., & Penev, S. (1999). On structural equation model equivalence. Multivariate Behavioral Research, 34, 199-244.
Stelzl, I. (1986). Changing a causal hypothesis without changing the fit: Some rules for generating equivalent path models. Multivariate Behavioral Research, 21, 309-331.

